Question
If A,B,C are three internal angles of a triangle, show that
\sin^3 A \cos (B – C) + \sin^3 B \cos (C – A) + \sin^3 C \cos (A – B) = 3 \sin A \sin B \sin C
Answer
Since A,B,C are three internal angles of a triangle
A = \pi-(B+C)
\sin A = \sin(B+C)
(1)
Apply the product to sum identity
\sin(B+C)\cos (B – C) = \dfrac{1}{2} [\sin(B+C+B-C ) +\sin(B+C - B-C) ]
Then we get
\sin(B+C)\cos (B – C) = \dfrac{1}{2} (\sin 2B+\sin 2C)
(2)
or
\sin A \cos (B – C) = \dfrac{1}{2} (\sin 2B+\sin 2C)
(3)
Apply the double angle identity for sines function. Then,
\sin A \cos (B – C) = \sin B\cos B+\sin C\cos C
(4)
So the first term of the expression on the left hand side is
\sin^3 A \cos (B – C) = \sin^2 A(\sin B\cos B+\sin C\cos C)
(5)
Similarly, we can deduce similar equations for the second and third terms.
\sin^3 B \cos (C – A) = \sin^2 B(\sin C\cos C+\sin A\cos A)
(6)
\sin^3 C \cos (A – B) = \sin^2 C(\sin A\cos A+\sin B\cos B)
(7)
Now apply the Laws of Sines, and let k be the ratio of sines to sides
\dfrac{\sin A}{a}= \dfrac{\sin B}{b} = \dfrac{\sin C}{c} =k
Then we can convert sines function to the multiples of sides.
\sin A = ka
(8)
\sin B = kb
(9)
\sin C = kc
(10)
So LHS is the sum of (5), (6), (7)
LHS = \sin^2 A(\sin B\cos B+\sin C\cos C)+ \sin^2 B(\sin C\cos C+\sin A\cos A)+ \sin^2 C(\sin A\cos A+\sin B\cos B)
=k^2a^2(kb\cos B+kc\cos C)+k^2b^2(kc\cos C+ka\cos A)+k^2c^2(ka\cos A+kb\cos B)
=k^3a^2(b\cos B+c\cos C)+k^3b^2(c\cos C+a\cos A)+k^3c^2(a\cos A+b\cos B)
Expand the brackets, regroup the terms and then factor out common factors
LHS = k^3[ab(a\cos B+b\cos A)+ac(a\cos C+c\cos A)+(b\cos C+c\cos B)]
Apply the projection law formulas
a=b\cos C+c\cos B
b=a\cos C+c\cos A
c=b\cos A+a\cos B
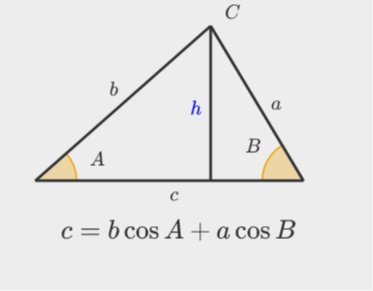
LHS = 3k^3abc
On the other hand, substitute (8), (9),(10) to RHS
RHS = 3 \sin A \sin B \sin C = 3k^3abc
which shows both sides are equal.