Ellipse

An ellipse is a regular oval shape that could be seen in our daily life, ellipse-shaped furniture, architecture or artworks. The earth rotates around the sun in an orbit that is not purely circular, but an elliptical one with an eccentricity of about 0.0167. Ellipse has been studied by mankind for thousands of years.

The-elliptical-orbit-of-a-planet-with-eccentricity-and-semi-major-axis

History of conic sections

As one of conic sections, ellipse could be traced back to Ancient Greece. It is believed that the first definition of a conic section was given by Menaechmus ( - 320 BC) as part of his effort to solve the Delian problem (Duplicating the cube). Menaechmus‘ definition lies in slicing a right circular cone with a plane that is orthogonal to the side of the cone. The conic section is the intersecting curve formed on the surface of the cone. It was found that the type of the conic section is dependent on the opening angle of the cone. If the angle is acute then it is an ellipse; if the angle is right then it is a parabola; and if the angle is obtuse then the conic section is a hyperbola.

Menaechmus' breakthrough left clue for discovery of later mathematicians. Apollonius of Perga (262 BC - 190 BC), known as The Great Geometer, made great advancement in the study of conics. Apollonius's study shows that any plane cutting a right circular cone, no matter its angle is orthogonal or not, will produce a conic section. The difference is the type of the conic. If the angle is less than the opening angle of the cone, the conic section will be ellipse. If the angle is equal to the opening angle of the cone, the conic section will be a parabola. If the angle is larger than the opening angle of the cone, the conic section will be a hyperbola. Apollonius gave the names ellipse (acutangle conic), parabola (rightangle conic) and hyperbola (obtusangle conic) for these curves, which we know today.

Definition as a locus of points

An ellipse could be taken as elongation of a circle. It is defined as the locus of all points in a plane such that the sum of their distances to the two focal points, is constant. The focal points are known as the foci (Latin way plural for focus) of the ellipse. The elongation of an ellipse is measured by its eccentricity e, which is defined as the ratio of the distances of a point on the ellipse to the focus, and the directrix, a line that is perpendicular to the major axis of symmetry. The eccentricity reflects how flat or round the shape of the ellipse is. For an ellipse, e < 1. If e=0, the two focal points overlap, the shape is a circle.

Ellipse equation

According to the definition, the sum of distances from any point P on the ellipse to two focal points F1 and F2, is a constant, which's designated as,

PF1+PF2=2a

(1)

where a is the semi-major axis, the longest diameter of the ellipse. The half of the corresponding shortest diameter of the ellipse is known as b. The midpoint C of the line segment joining the foci is the center of the ellipse. Then in Cartesian coordinates, the foci are given as F1(-c,0), F2(c,0) and the point P (x,y).

Derivation of Ellipse equation

Apply the distance formula between two points to (1),

\sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2}=2a

(2)

Move the second radical from the left hand side of (2) to its right hand side:

\sqrt{(x+c)^2+y^2}=2a-\sqrt{(x-c)^2+y^2}

Square both sides of the equation

(x+c)^2+y^2 = 4a^2-4a\sqrt{(x-c)^2+y^2}+(x-c)^2+y^2

Cancel the like terms and simplify

\sqrt{(x-c)^2+y^2} = a-\dfrac{c}{a}x

(3)

Square both sides again to remove the square root,

(x-c)^2+y^2 = (a-\dfrac{c}{a}x)^2

x^2-2cx+c^2+y^2 = a^2-2cx+\dfrac{c^2}{a^2}x^2

Cancel like terms and group x terms

\Big( \dfrac{a^2-c^2}{a^2} \Big) x^2+y^2 = a^2-c^2

(4)

Noticed |a|>|c|, let

b^2 = a^2-c^2

(5)

The equation (4) is transformed to,

\dfrac{b^2}{a^2}x^2+y^2 = b^2

Dividing the equation by b^2 gives the equation of the ellipse.

\dfrac{x^2}{a^2} +\dfrac{y^2}{b^2}=1

(6)

Why is b the semi-minor axis of the ellipse

The parameter b defined in (5) is actually the semi-minor axis of the ellipse. In the figure above, move point P to make it intersection point of axis y and the ellipse, then \triangle PF1F2 becomes an isosceles triangle, that is

PF1 = PF2

Substituting the equation (1), which is from the definition of the ellipse yields

PF1 = PF2=a

(7)

When P is on the axis y, \triangle PCF1 is a right triangle. Using the Pythagorean Theorem,

PC^2 = PF1^2-CF1^2

that is,

PC^2 = a^2-c^2

(8)

Comparing the equation (8) with (5) shows

PC = b

It's indeed b is the semi-minor axis of the ellipse. It should be noted the minor axis of the ellipse must not be always on axis y. It could be on axis x or any inclined line by rotation of the ellipse.

Rotation of the ellipse

Rotating the ellipse (6) by θ clockwise gives the following equation in a new coordinates.

\dfrac{u^2}{a^2} +\dfrac{v^2}{b^2}=1

(9)

where

\begin{aligned} \begin{pmatrix} u \\ v \end{pmatrix} &=\begin{pmatrix} \cosθ & -\sinθ \\ \sinθ & \cosθ \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \\ &= \begin{pmatrix} x\cos\theta -y\sin\theta \\ x\sin\theta + y\cos\theta \end{pmatrix} \end{aligned}

Substituting u and v into equation (9) gives general formula for an ellipse after rotating an angle of θ.

\dfrac{(x\cos\theta -y\sin\theta)^2}{a^2} +\dfrac{(x\sin\theta + y\cos\theta )^2}{b^2}=1

(10)

If θ=90\degree, the equation is simplified as

\dfrac{y^2}{a^2}+\dfrac{x^2}{b^2} = 1

(11)

Since |a| >|b|, the major axis lies on the axis y, and mior axis on axis x.

Parametric form of ellipse equation

A circle that is centered at (0,0) could be represented parametric form as below

\begin{aligned} x&= r\cos \theta \\ y&=r\sin\theta \end{aligned}

where x,y is the coordinates of any point on the circle, r is the radius of the circle, \theta is the angle made by the radius with axis x.

The curve of an ellipse could also be expressed in parametric form analogous to that of a circle.

\begin{aligned} x&= a\cos t \\ y&=b\sin t \end{aligned}

(12)

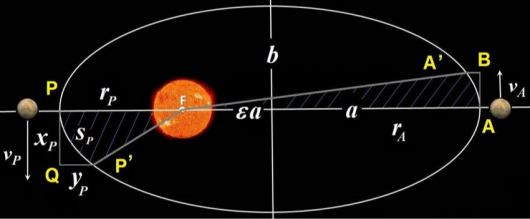
The parameter t is not the angle formed by the line joining the point P and center of the ellipse with the axis x, but determined geometrically in the figure. A line segment joining point A on a circle with radius a has intersection with the circle with radius b at point B. A line that passes point B and is parallel to major axis has intersection with the ellipse at point P. Then Point P could be represented in parametric form using the trigonometric functions of the angle t formed by AB with major axis.

In astronomy, the angle t is called the eccentric anomaly, an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit.

Ellipses in Polar Coordinates

The equation of an ellipse could also be represented in polar coordinates in terms of variables expressed in radial and angular coordinates. Assuming the case when the polar coordinates is centered at focus F1, the radius r makes the angle \theta with major axis, which is on the positive real axis.

The ellipse definition implies that

\|r\|+\|F2P\| = 2a

(13)

r = \|r\| implies \|r-2a \| = \|F2P\|, then

(r-2a)^2 = (\|F2P\|)^2

(14)

According to our assumption, the coordinates of point P and F2 are given as P (r,θ) and F2(2c,0).

Apply the distance formula from the polar coordinate system for (14)

(r-2a)^2 = r^2+(2c)^2-4rc\cos \theta

(15)

Expand the square and simply,

r^2-4ra+4a^2 = r^2+4c^2-4rc\cos\theta

-4ra+4a^2 = 4c^2-4rc\cos\theta

-ra+a^2 = c^2-rc\cos\theta

Solve for r,

-ra+rc\cos\theta = c^2-a^2

(-a+c\cos\theta)r = c^2-a^2

r = \dfrac{ c^2-a^2}{-a+c\cos\theta}

(16)

Let

b^2 = a^2-c^2

r = \dfrac{b^2}{a-c\cos\theta }

(17)

Dividing the fraction expression on the right hand side by a yields

r = \dfrac{b^2/a}{1-c/a\cdot \cos\theta }

\quad = \dfrac{l}{1-e \cos\theta }

(18)

where l =\dfrac{b^2}{a} , which is the semi-latus rectum of the ellipse and e = \dfrac{c}{a} , which is the eccentricity of the ellipse.

Why is the conic section ellipse

Apollonius of Perga found the conic will be an ellipse when slicing a right circular cone with a plane at angle that is is less than the opening angle of the cone. How to prove the conic section formed is an ellipse? The Dandelin spheres were discovered by the French mathematician Germinal Pierre Dandelin to give an elegant proof of the statement. The same method is also used for the proof for other conic sections, such as parabola and hyperbola.

Dandelin spheres are spheres inside a right circular cone such that it keeps tangent to both the surface of the cone and the plane that is slicing the cone. For ellipse and hyperbola, two spheres are needed for the proof. For parabola, only one sphere is needed. The introduction of Dandelin spheres makes the proof of conic sections intuitive and straightforward. We are going to show how Dandelin spheres could facilitate the proof below.

In the figure above, the plane e slices the right circular cone S so that it is tangent to both spheres that are kept tangent with the surface of the cone. The tangent point between the plane and the sphere G1 is at point F1. The tangent point between the plane and the sphere G2 is at point F2. To prove the intersecting curve formed by the plane and the cone is an ellipse is to prove that the distances from any point on the curve to the two tangent points are consistent.

Before moving forward, let's recognize the two premises which are important to our next steps.

First, all the tangent points formed by a Dandelin sphere and the cone forms a circle that is parallel to the base of the cone. More specifically, if the plane is parallel to the base then the body below is a conical frustum. 2 Dandelin spheres forms frustum between them. We are going to use the property that all the generatrix lines of the frustum are equal in their length.

Second, all the tangent points from an external point to a sphere forms a circle. The distances from an external point to different tangent points on a sphere are equal. This is similar to the tangent lines to a circle in 2D plane. The distance from a point to two tangent points to a circle are equal.

Now let's continue our proof. Arbitrarily plot a generatrix line from the vertex S to the base of the cone. The line intersects the intersecting circle by sphere G1 at point P1, the intersecting circle by sphere G2 at point P2 and the conic section (or plane e) at point P.

Since P1 and F1 are two tangent points from point P to sphere G1, then we know the two line segments are equal in their length.

PF1 = PP1

(19)

Similarly, the two tangent line segments from P to sphere G2 are also equal in length.

PF2 = PP2

(20)

Addition of (19) and (20) yields

PF1+PF2 = PP1+PP2 = P1P2

Since P1P2 is the generatrix of the frustum, which is consistent in length, we have proved the statement. The distance from any point on the conic section to foci is consistent in length. More specifically, when the point P is at the vertex, the point of intersection of the ellipse with its axis of symmetry,

PF1+PF2 = 2a

(21)

if a is defined as the length of semi-major axis of the ellipse.

Collected in the board: Conic sections

Steven Zheng posted 1 year ago